Easy Sudoku solving techniques
In the first part of the Sudoku series, we built a Sudoku Solver. Next is the Sudoku generator: a program that can generate games of different difficulty, ideally automated, new games every day., meaning a program that produces easy, medium, and hard Sudokus (yes, there are also Diabolical and Extreme Sudokus but these are out of my league sorry).
But what is the difference between an easy, medium, and hard Sudoku? The techniques needed to solve them. Yes, easy Sudokus have more givens (start numbers) but it’s not possible to classify a Sudoku only by the number of givens.
My initial (naive) idea of generating the Sudoku was this:
- Start with an empty board and fill some squares
- Solve the puzzle with the solver
- Remove some of the numbers (over 50)
Piece of cake right? Not quite. Using the above algorithm it is easy to generate puzzles that are almost impossible to solve, or at least harder than they need to be. Why? Because they can be solved only by using some crazy techniques you never heard of like 3D Medusa or Sue-de-Cog.
So I need to implement the same techniques a human would use to solve the puzzle and check if the puzzle is solvable by these techniques.
The new algorithm does the following:
- Starts with an empty board, and fills the first, middle, and last 3x3 boxes with random numbers from 1 to 9.
- Uses the solver to solve the puzzle and fill the board with all the numbers.
- Removes some of the numbers (about 53-57). After each number is removed, it checks if the puzzle is still solvable using the easy sudoku techniques detailed here:
- Naked/Hidden Singles (Lone rangers)
- Naked/Hidden pairs (Twins)
- Naked/Hidden Triples
- Pointing pairs
- Box/line reduction
Want to see them in action?

Why these techniques? Because these are basic Sudoku-solving techniques. I think every person that likes to solve Sudokus knows them. Maybe not by the name since they tend to have different names all over the globe, but I’m sure everyone gets the gist of them. I’m using the British Andrew Stuart’s terminology.
There is one thing we need to implement first, something that is very handy, the pencil marks used to show what digits can go in each cell/square, the square candidates.
Pencil marks
If only one number can go into a cell(square), it means that number is the solution for that cell. But when you solve a Sudoku more often than not you realize that in a certain cell can go two, three, or more numbers. We call candidates the numbers that can be the solution of a cell.
Here is an example where we display all the candidates in all empty cells:
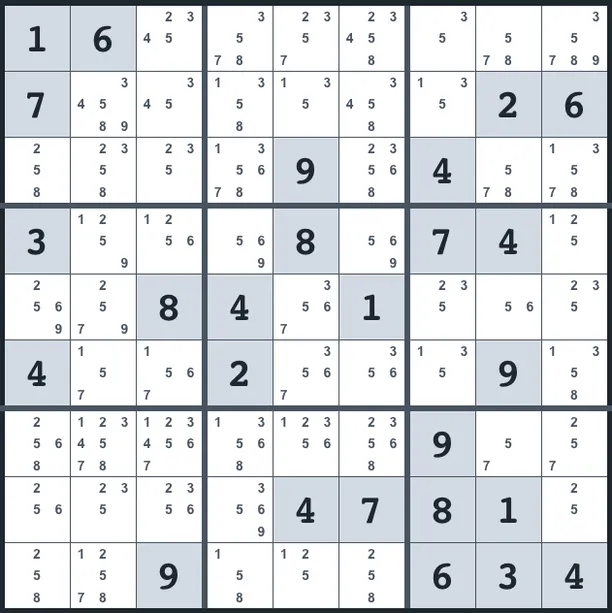
At first glance, these candidates don’t look very helpful, and indeed most people don’t bother to enter candidates in a cell(square) when they are more than 3. But don’t be fooled, candidates are extremely important in solving any non-trivial Sudoku.
At least from an algorithm view, solving a Sudoku means reducing the candidates over and over until there is one candidate left. All the techniques presented below are based on candidates: how many candidates are in a cell(square) and how candidates from a row/column/box influence candidates in other rows/columns/boxes.
How are the candidates determined? To find the candidates one has to check each cell’s row, column, and box to find the cells’ numbers: a number present on the cell‘s row/column/box cannot be the cell’s solution.
Note that I use cell and square as the same thing, one of the board’s 81 parts.
/**
* Returns the grid candidates
* @param {*} grid Grid object, keys are cell names (A1, B2...)
* and values are the cell numbers (0,1,..,9).
* Empty cells have value 0 or '0'
* @param {*} candidates Current candidates
* @returns Candidates object, keys are cell names (A1, B2...),
* values are cell candidates string ("1235", "23", etc)
*/
export function findCandidates(grid, candidates) {
const peers = {};
Object.keys(grid).forEach(sq => {
// find all squares that are not equal to sq
const peerSqs = units[sq].map(u => u.filter(s => s != sq)).flat();
peers[sq] = [...peerSqs];
});
// initially candidates are not available
if(!candidates) {
candidates = {};
squares.forEach(sq => { candidates[sq] = digits });
}
Object.keys(grid).forEach(sq => {
if(grid[sq] !== 0 && grid[sq] !== '0') {
candidates[sq] = '';
// remove value from peers
peers[sq].forEach(p => {
candidates[p] = candidates[p].replace(grid[sq], "");
})
}
})
return candidates;
}
I’ve detailed in the Sudoku Solver what data models I use. Please take a look there if you don’t understand what peers, units, and unitlists are.
Naked/Hidden singles
When there is only one candidate in a cell, that candidate is the solution for the cell. We call that candidate a “naked single”. Others (I wonder who) call it “lone ranger”.
I’ve highlighted for your benefit one of the candidates:
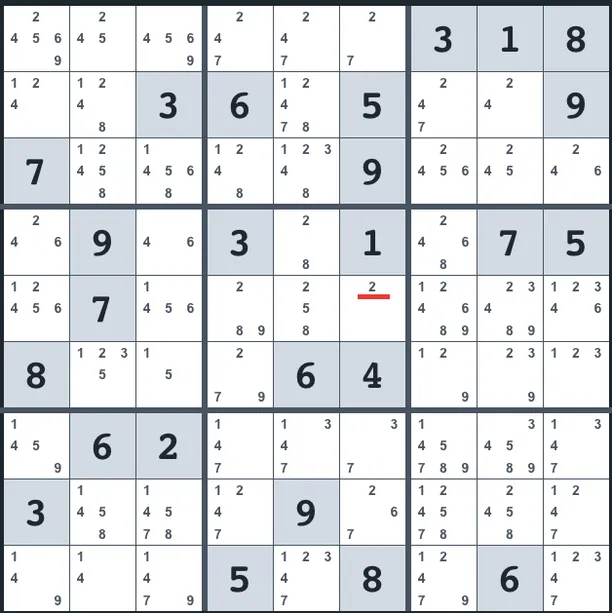
This is the ideal (easiest) case.
But there is another case, when the “single” candidate is hidden between other candidates, making it much harder to spot. Here are a bunch of hidden singles:
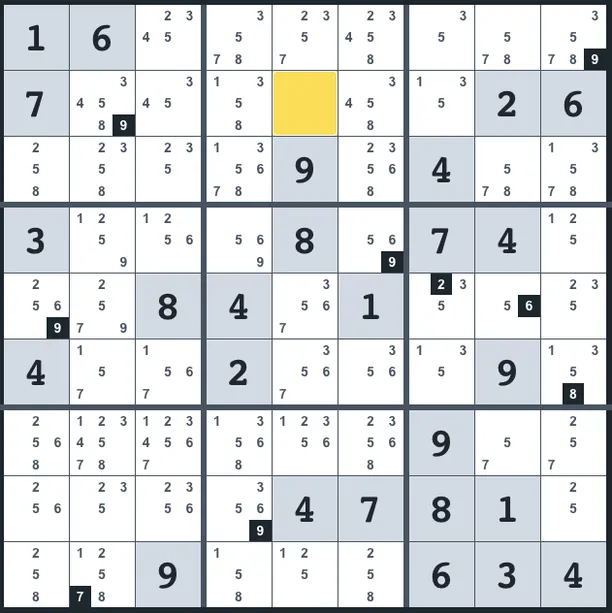
Spotting singles is the most important technique because they are the solution. You can add the solution to a cell only when you’re certain only a single number can go in that cell.
/**
* Returns all singles on the board
* @param {*} candidates Candidates object, keys are cell names (like A1, B2)
* and values are strings with candidates like "1239"
* @returns Object where keys are cell names and values are the single candidate
*/
export function findSingles(candidates){
const result = {};
unitlist.forEach(unit => {
const numberCounts = {1:0,2:0,3:0,4:0,5:0,6:0,7:0,8:0,9:0};
// combine all candidates for each square in unit in one big string (e.g 1234123617829563)
const unitCandidates = unit.reduce((all, sq) => candidates[sq].length > 0 ? all+candidates[sq]: all, '');
// count how many of each digit we have
[...unitCandidates].forEach(digit => numberCounts[digit]++);
// check if one digit is present only once
Object.keys(numberCounts).forEach(key => {
if(numberCounts[key] === 1){
const sq = unit.find(sq => candidates[sq].includes(`${key}`));
result[sq] = key;
}
})
})
// naked singles
for(let cn in candidates){
if(candidates[cn].length === 1) result[cn] = candidates[cn];
}
return result;
}
Naked/Hidden pairs
When two numbers(candidates) are present only in the same two cells of a row/column/box, it means the two numbers can only go in those two cells — even if we don’t know in which way yet.
Note: If a candidate must go in certain cells then the candidate cannot go in the rest of the row/column/box cells.
The important thing is that all the other cells from the pair’s row/column/box cannot contain the candidates we’ve fixed in a pair of cells. Thus we can reduce candidates from cells — we remove the candidates from cells that cannot have them.
This is the purpose of all techniques discussed here — except “naked/hidden singles” — they reduce candidates. They reduce and reduce until there are singles - until we can fill empty cells with correct numbers.
In the following example we have a naked pair (8 and 9) and a hidden pair (2 and 4):

Note: We label the rows from top to bottom A to I, and columns from left to right 1 to 9. So the first square of the boars, in the top left corner is A1, and the last, in the bottom right corner, is I9.
An explanation for the pair 8-9:
- 8 and 9 can only go in cells B5 and B6 on row B (they cannot go on B1 and B7 because there is an 8 in the corresponding boxes)
- All other candidates from the two cells can be removed. B5 and B6 can only take 8 or 9.
Again, please note that using this technique we can’t fill empty cells — we don’t know in which cell will go the 8 or the 9), what we do is remove other candidates.
The explanation for 2-4:
- 2 and 4 can only go in cells G9 and H9 on column 9 (there are 2s and 4s on columns 7 and 8, so 2 and 4 can go only on column 9)
- All other candidates from the two cells can be removed. G9 and H9 can only take 2 or 4.
/**
* Returns all candidates that remove candidates and candidates to be removed
* @param {*} candidates Candidates object, keys are cell names (like A1, B2)
* and values are strings with candidates like "1239"
* @returns {candidatesToHighlight, candidatesToRemove} candidatesToHighlight is
* an object where keys are cell names and values are the single candidate,
* candidatesToRemove is an object where keys are cell names and values are the candidate strings
*/
export function findPairs(candidates){
const result = {
candidatesToHighlight: {},
candidatesToRemove: {}
};
unitlist.forEach(unit => {
const numberCounts = {1:0,2:0,3:0,4:0,5:0,6:0,7:0,8:0,9:0};
// combine all candidates for each square in unit in one big string
const unitCandidates = unit.reduce((all, sq) => candidates[sq].length > 1 ? all+candidates[sq]: all, '');
// count how many of each digit we have
[...unitCandidates].forEach(digit => numberCounts[digit]++);
const doubleCandidates = [];
Object.keys(numberCounts).forEach(key => {
if(numberCounts[key] === 2){
doubleCandidates.push(key);
}
})
// if at least 2 digits are present twice
if(doubleCandidates.length === 2){
// grup candidates in pairs
const pairs = doubleCandidates.flatMap((val, index) => doubleCandidates.slice(index+1).map( w => [val,w] ));
pairs.forEach(pair => {
const squaresWithPairCandidates = unit.filter(sq => candidates[sq].includes(pair[0]) && candidates[sq].includes(pair[1]) );
if(squaresWithPairCandidates.length === 2) {
const candidatesToRemove = {};
const pairsToAdd = {};
const firstSquareUnits = units[squaresWithPairCandidates[0]];
const secondSquareUnits = units[squaresWithPairCandidates[1]];
// find the units(row/col/box) that contain both squaresWithPairCandidates
const intersection = firstSquareUnits.filter(unit => {
// need to transform the unit array to a string
return secondSquareUnits.map(u => u.join('')).includes(unit.join(''));
})
// remove the pair from all unit square's candidates
intersection.forEach(unit => {
unit.forEach(square => {
if(!squaresWithPairCandidates.includes(square)) {
const toRemove = (candidates[square].includes(pair[0], '') ? pair[0] : '') +
(candidates[square].includes(pair[1], '') ? pair[1] : '')
if(toRemove.length > 0) {
candidatesToRemove[square] = toRemove;
}
}
})
})
squaresWithPairCandidates.forEach(sq => {
pairsToAdd[sq] = pair.join('');
// the rest of square candidates must be removed
const toRemove = candidates[sq].replace(pair[0], '').replace(pair[1], '');
if(toRemove.length > 0) {
candidatesToRemove[sq] = toRemove;
}
});
// use the pair only if we can remove some candidates
if(Object.keys(candidatesToRemove).length !== 0) {
for(let p in pairsToAdd) {
if(!result.candidatesToHighlight[p]) result.candidatesToHighlight[p] ='';
result.candidatesToHighlight[p] = pairsToAdd[p];
}
for(let c in candidatesToRemove) {
if(!result.candidatesToRemove[c]) result.candidatesToRemove[c]='';
result.candidatesToRemove[c] = candidatesToRemove[c];
}
}
}
});
}
})
return result;
}
Naked/Hidden triples
Triples (triple candidates) are also useful, even though it is a bit harder to see them. We can extend the pairs technique to triples, but instead of the two squares that make the pair, we need to look for three squares that are present only in two or three squares from a row/column/box.
The idea is that if three candidates are present only in three squares, only those candidates can be in those squares and cannot be in the row/column/box that contains the triple (if any).
The combinations of candidates for a triple are:
- XYZ XYZ XYZ - all three candidates are present in three cells/squares.
- XYZ XYZ XY - all three candidates are present in two cells and two out of three are present in the third cell.
- XYZ XY YZ - all three candidates are present in a cell, and combinations of them are present in two cells.
- XY YZ XZ - each combination of them is present in a different cell.
Just as pairs, we can have naked or hidden triples. Let’s see an example of a naked triple:

Candidates 3, 5, and 8 are present only in three cells in box 1. So we can safely remove the 3s, 5s and 8s from the rest of the candidates from column 1. In this case, we have an XYZ XY YZ type of combination.
Here is another example with hidden triples. These are powerful because they also remove the candidates from their own cells.

This is the most complicated code, those combinations killed me.
function combinations3(nrs) {
const result = [];
for(let i=0; i<nrs.length;i++) {
for(let j=i+1; j<nrs.length;j++) {
for(let k=j+1; k<nrs.length;k++) {
result.push( [ nrs[i], nrs[j], nrs[k] ]);
}
}
}
return result;
}
/**
* Returns all candidates that remove candidates and candidates to be removed
* @param {*} candidates Candidates object, keys are cell names (like A1, B2)
* and values are strings with candidates like "1239"
* @returns {candidatesToHighlight, candidatesToRemove} candidatesToHighlight is an
* object where keys are cell names and values are the single candidate,
* candidatesToRemove is an object where keys are cell names and values are the candidate strings
*/
export function findTriples(candidates){
const result = {
candidatesToHighlight: {},
candidatesToRemove: {}
};
unitlist.forEach(unit => {
const numberCounts = {1:0,2:0,3:0,4:0,5:0,6:0,7:0,8:0,9:0};
// combine all candidates for each square in unit in one big string
const unitCandidates = unit.reduce((all, sq) => candidates[sq].length > 1 ? all+candidates[sq]: all, '');
// count how many of each digit we have
[...unitCandidates].forEach(digit => numberCounts[digit]++);
const candidatesIn2or3Cells = [];
Object.keys(numberCounts).forEach(key => {
if(numberCounts[key] === 2 || numberCounts[key] === 3){
candidatesIn2or3Cells.push(key);
}
})
const triples = combinations3(candidatesIn2or3Cells);
triples.forEach(triple => {
// find squares that have the combinations
const sq1 = unit.find(sq => (candidates[sq].includes(triple[0]) && candidates[sq].includes(triple[1])));
const sq2 = unit.filter(sq => sq!== sq1).find(sq => (candidates[sq].includes(triple[0]) && candidates[sq].includes(triple[2])));
const sq3 = unit.filter(sq => sq!== sq1 && sq!==sq2).find(sq => (candidates[sq].includes(triple[1]) && candidates[sq].includes(triple[2])));
const sqsWithAll = unit.filter(sq => candidates[sq].includes(triple[0]) || candidates[sq].includes(triple[1]) || candidates[sq].includes(triple[2]));
if(sqsWithAll.length === 3 && sq1 && sq2 && sq3) {
const candidatesToRemove = {};
const pairsToAdd = {};
sqsWithAll.forEach(sq => {
pairsToAdd[sq] = triple.join('');
const reducedCandidates = candidates[sq].replace(triple[0], '').replace(triple[1], '').replace(triple[2], '');
if(reducedCandidates && candidatesToRemove[sq] !== reducedCandidates) candidatesToRemove[sq] = reducedCandidates;
});
const firstSquareUnits = units[sqsWithAll[0]];
const secondSquareUnits = units[sqsWithAll[1]];
const thirdSquareUnits = units[sqsWithAll[2]];
// find the units(row/col/3x3 box) that contain all 3 squares
let intersection = firstSquareUnits.filter(unit => {
// need to transform the unit array to a string
return secondSquareUnits.map(u => u.join('')).includes(unit.join(''));
}).filter(unit => {
return thirdSquareUnits.map(u => u.join('')).includes(unit.join(''));
})
intersection.forEach(unit => {
unit.forEach(square => {
if(!sqsWithAll.includes(square) && candidates[square]) {
const reducedCandidates = candidates[square].replace(triple[0], '').replace(triple[1], '').replace(triple[2], '');
if(reducedCandidates !== candidates[square]) {
if(!candidatesToRemove[square]) candidatesToRemove[square] =''
candidatesToRemove[square] += triple.join('');
}
}
})
})
// use the pair only if we can remove some candidates
if(Object.keys(candidatesToRemove).length !== 0) {
for(let p in pairsToAdd) {
if(!result.candidatesToHighlight[p]) result.candidatesToHighlight[p]=''
result.candidatesToHighlight[p] = pairsToAdd[p];
}
for(let c in candidatesToRemove) {
if(!result.candidatesToRemove[c]) result.candidatesToRemove[c]= ''
result.candidatesToRemove[c] += candidatesToRemove[c];
}
}
}
})
});
return result;
}
Pointing pairs
We look at each box. If there is a box candidate that is present only inside a row/column, we can safely remove that candidate from the rest of the row/column.
In this example, box 3 has candidate 9 only in column 7(in A7 and C7). This means that
7 will go in either A7 or C7. But this also means there cannot be any 9s on the rest of
the column 7, so we can remove the other 9s from the column:
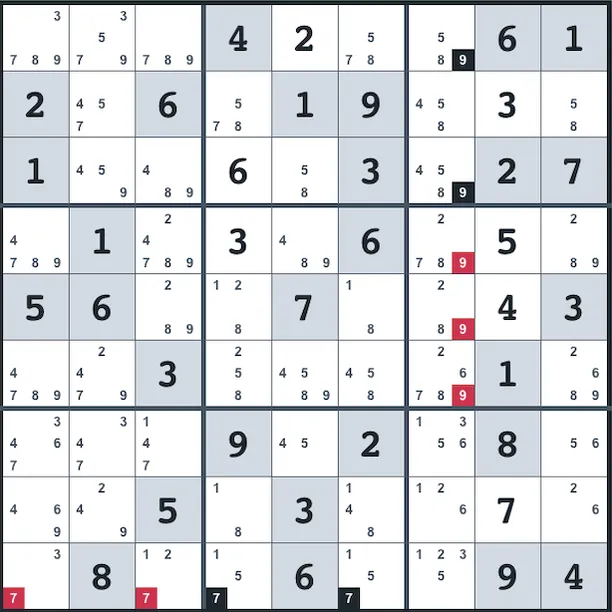
Here is the code.
/**
* Returns all candiates that remove candidates and candidates to be removed
* @param {*} candidates Candidates object, keys are cell names (like A1, B2)
* and values are strings with candidates like "1239"
* @returns {candidatesToHighlight, candidatesToRemove} candidatesToHighlight is an
* object where keys are cell names and values are the single candidate,
* candidatesToRemove is an object where keys are cell names and values are the candidate strings
*/
export function findPoitingPairs(candidates){
const result = {
candidatesToHighlight: {},
candidatesToRemove: {}
};
// we're intersted only in boxes this time
const boxes = unitlist.filter((v, index) => index >= 18);
boxes.forEach(unit => {
const numberCounts = {1:0,2:0,3:0,4:0,5:0,6:0,7:0,8:0,9:0};
// combine all candidates for each square in unit in one big string
const unitCandidates = unit.reduce((all, sq) => candidates[sq].length > 1 ? all+candidates[sq]: all, '');
// count how many of each digit we have
[...unitCandidates].forEach(digit => numberCounts[digit]++);
const multipleCandidates = [];
Object.keys(numberCounts).forEach(key => {
if(numberCounts[key] === 2 || numberCounts[key] === 3){
multipleCandidates.push(key);
}
})
// check if all candidates are on same row or same column
multipleCandidates.forEach(candidate => {
const candidatesSquares = unit.filter(sq => candidates[sq].includes(candidate));
// all square name start with same letter A, B, C...
const sameRow = new Set(candidatesSquares.map(sq => sq[0])).size === 1;
if(sameRow) {
const row = units[candidatesSquares[0]][1];
const candidatesToRemove = row.filter(sq => !candidatesSquares.includes(sq)).filter(sq => candidates[sq].includes(candidate));
if(candidatesToRemove.length > 0) {
candidatesSquares.forEach(sq => {
if(!result.candidatesToHighlight[sq]) result.candidatesToHighlight[sq]= '';
result.candidatesToHighlight[sq] += candidate;
})
candidatesToRemove.forEach(sq => {
if(!result.candidatesToRemove[sq]) result.candidatesToRemove[sq] ='';
result.candidatesToRemove[sq] += candidate;
})
}
}
else {
// all square name start with same digit 1, 2, 3...
const sameCol = new Set(candidatesSquares.map(sq => sq[1])).size === 1;
if(sameCol) {
const col = units[candidatesSquares[0]][0];
const candidatesToRemove = col.filter(sq => !candidatesSquares.includes(sq)).filter(sq => candidates[sq].includes(candidate));
if(candidatesToRemove.length > 0) {
candidatesSquares.forEach(sq => {
if(!result.candidatesToHighlight[sq]) result.candidatesToHighlight[sq]= '';
result.candidatesToHighlight[sq] += candidate;
})
candidatesToRemove.forEach(sq => {
if(!result.candidatesToRemove[sq]) result.candidatesToRemove[sq] ='';
result.candidatesToRemove[sq] += candidate;
})
}
}
}
})
});
return result;
}
Box/Line reduction
This is very similar to pointing pairs, but instead of looking at boxes are removing candidates from rows/columns, we look at lines(rows/columns) are remove candidates from boxes.
In column 2, candidate 2 is present only in box 1 (A2 and B2). Thus the box needs to contain a 2 in one of those cells and it cannot have 2 in the rest of the cells.
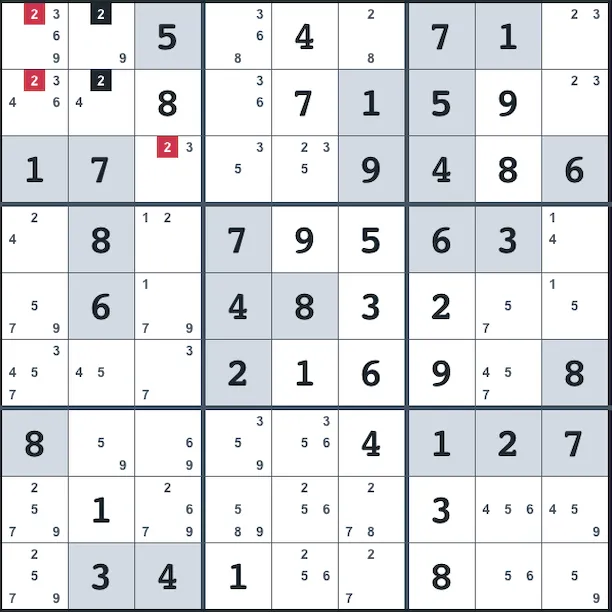
Here it is, in all its glory.
/**
* Returns all candidates that remove candidates and candidates to be removed
* @param {*} candidates Candidates object, keys are cell names (like A1, B2)
* and values are strings with candidates like "1239"
* @returns {candidatesToHighlight, candidatesToRemove} candidatesToHighlight is an
* object where keys are cell names and values are the single candidate,
* candidatesToRemove is an object where keys are cell names and values are the candidate strings
*/
export function findBoxLinePairs(candidates){
const result = {
candidatesToHighlight: {},
candidatesToRemove: {}
};
// we're intersted only in rows/colums this time
const rowAndCols = unitlist.filter((v, index) => index < 18);
rowAndCols.forEach((unit, index) => {
const numberCounts = {1:0,2:0,3:0,4:0,5:0,6:0,7:0,8:0,9:0};
// combine all candidates for each square in unit in one big string
const unitCandidates = unit.reduce((all, sq) => candidates[sq].length > 1 ? all+candidates[sq]: all, '');
// count how many of each digit we have
[...unitCandidates].forEach(digit => numberCounts[digit]++);
const multipleCandidates = [];
Object.keys(numberCounts).forEach(key => {
if(numberCounts[key] === 2 || numberCounts[key] === 3){
multipleCandidates.push(key);
}
})
// check if all candidates are on same row or same column
multipleCandidates.forEach(candidate => {
const candidatesSquares = unit.filter(sq => candidates[sq].includes(candidate));
// get one square box, for example the first square box
const boxSquares = units[candidatesSquares[0]][2];
const sameBox = candidatesSquares.reduce((all, current) => all && boxSquares.includes(current), true);
if(sameBox) {
const candidatesToRemove = boxSquares.filter(sq => !candidatesSquares.includes(sq) && candidates[sq].includes(candidate));
if(candidatesToRemove.length > 0) {
candidatesSquares.forEach(sq => {
if(!result.candidatesToHighlight[sq]) result.candidatesToHighlight[sq]='';
result.candidatesToHighlight[sq] = candidate;
})
candidatesToRemove.forEach(sq => {
if(!result.candidatesToRemove[sq]) result.candidatesToRemove[sq] ='';
result.candidatesToRemove[sq] += candidate;
})
}
}
// all square name start with same letter A, B, C...
const sameRow = new Set(candidatesSquares.map(sq => sq[0])).size === 1;
if(sameRow) {
const row = units[candidatesSquares[0]][1];
const candidatesToRemove = row.filter(sq => !candidatesSquares.includes(sq)).filter(sq => candidates[sq].includes(candidate));
if(candidatesToRemove.length > 0) {
candidatesSquares.forEach(sq => {
if(!result.candidatesToHighlight[sq]) result.candidatesToHighlight[sq]= '';
result.candidatesToHighlight[sq] += candidate;
})
candidatesToRemove.forEach(sq => {
if(!result.candidatesToRemove[sq]) result.candidatesToRemove[sq] ='';
result.candidatesToRemove[sq] += candidate;
})
}
}
else {
// all square name start with same digit 1, 2, 3...
const sameCol = new Set(candidatesSquares.map(sq => sq[1])).size === 1;
if(sameCol) {
const col = units[candidatesSquares[0]][0];
const candidatesToRemove = col.filter(sq => !candidatesSquares.includes(sq)).filter(sq => candidates[sq].includes(candidate));
if(candidatesToRemove.length > 0) {
candidatesSquares.forEach(sq => {
if(!result.candidatesToHighlight[sq]) result.candidatesToHighlight[sq]= '';
result.candidatesToHighlight[sq] += candidate;
})
candidatesToRemove.forEach(sq => {
if(!result.candidatesToRemove[sq]) result.candidatesToRemove[sq] ='';
result.candidatesToRemove[sq] += candidate;
})
}
}
}
})
});
return result;
}
That’s the last one, finally.
Putting them all together
To solve the puzzle, the techniques must be called in a specific order:
- First, we always need to check if there are singles because they are the solving progress
- Next, we use techniques based on algorithm difficulty. This is a bit controversial, as I think the triples is the most complex one, at least in my implementation.
- If a technique yields results, we remove those candidates and restart from checking singles, yes using a recursive function (one of those things I was supposed to use only in school)
function isGridSolved(grid) {
return Object.keys(grid).reduce((result, sq) => result && grid[sq]!= 0, true);
}
function solveGrid(grd, cndts){
let found = true;
while(found) {
const hiddenSingles = findSingles(cndts);
const hiddenSinglesKeys = Object.keys(hiddenSingles);
if(hiddenSinglesKeys.length > 0) {
Object.keys(hiddenSingles).forEach(sq => {
grd[sq] = hiddenSingles[sq];
})
cndts = findCandidates(grd, cndts);
} else{
found = false;
}
}
const solved = isGridSolved(grd);
if(solved) {
return true;
}
let result = findPairs(cndts);
if(Object.keys(result.candidatesToRemove).length > 0) {
removeCandidates(cndts, result.candidatesToRemove);
return solveGrid(grd, cndts);
}
result = findTriples(cndts);
if(Object.keys(result.candidatesToRemove).length > 0) {
removeCandidates(cndts, result.candidatesToRemove);
return solveGrid(grd, cndts);
}
result = findPoitingPairs(cndts);
if(Object.keys(result.candidatesToRemove).length > 0) {
removeCandidates(cndts, result.candidatesToRemove);
return solveGrid(grd, cndts);
}
result = findBoxLinePairs(cndts);
if(Object.keys(result.candidatesToRemove).length > 0) {
removeCandidates(cndts, result.candidatesToRemove);
return solveGrid(grd, cndts);
}
return isGridSolved(grd);
}
The Sudoku generator then works like this:
function generate() {
// start from empty
let grid = emptyGrid();
iterator = null;
function cross(A, B){
return A.map(a => B.map(b => a+b)).flat();
}
// fill first, middle and last boxes
const boxRows = [['A','B','C'], ['D','E','F'], ['G','H','I']];
const boxCols = [['1','2','3'], ['4','5','6'], ['7','8','9']];
for(let i=0;i<3;i++) {
const sqs = cross(boxRows[i],boxCols[i]);
const sorted = [1,2,3,4,5,6,7,8,9].sort((a, b) => 0.5 - Math.random());
sqs.forEach(sq => {
grid[sq] = sorted.pop();
})
}
// solve the grid
grid = solve(toLine(grid));
// remove cells as many as possible
const emptySquares = [];
let tries = 0;
let count = 1;
let currentGrid = {...grid};
const LIMIT = 60;
while(emptySquares.length < LIMIT && tries < 200) {
tries++;
if(emptySquares.length >= LIMIT) {
tries = 200;
break;
}
// pick a random cell and try to remove it
let row = Math.floor(Math.random() * (9 - 1 + 1) + 1);
let col = Math.floor(Math.random() * (9 - 1 + 1) + 1);
let position = rows[row-1]+cols[col-1];
if(!emptySquares.includes(position)) {
let gridToTry = {...currentGrid};
gridToTry[position] = "0";
const cnds = findCandidates(gridToTry);
// try to solve the grid without the removed cell
if(solveGrid({...gridToTry}, cnds)){
emptySquares.push(position);
currentGrid = {...gridToTry};
}
}
}
return grid;
});
Again, if you want to see it in action, I’m very proud of it :) Easy Sudoku solving techniques
Of course, I need to write unit tests for each function (which as you can see is as pure as it gets, so it will be easy to test). And then refactor and refine the code because it has a lot of duplications.
After that we’ll try to implement the medium sudoku techniques:
- X-Wing
- Simple Colouring
- Y-Wing
- Swordfish
- XYZ Wing
- BUG